Matematyka jest z nami od tysięcy lat, a liczba zero jest fundamentem nauczania matematyki w dzisiejszym świecie. Jednak, niezależnie jak abstrakcyjnie to zabrzmi, zero kiedyś wcale nie istniało.
 

Europejska myśl matematyczna

 
Jak się okazuje Europejczycy nie posługiwali się powszechnie zerem, aż do XII wieku naszej ery (1). Do użytku w Europie wprowadził go dopiero znany włoski matematyk Leonardo z Pizy, czyli Fibonacci. Ojciec młodego Pisano był bogatym kupcem, a młody Leonardo podróżował z nim w interesach do krajów świata arabskiego. To właśnie tam zapoznał się z hindusko-arabskim systemem numerycznym. Fibonacci uznał, że działania arytmetyczne przeprowadzane w tym nowym systemie są zdecydowanie bardziej poręczne niż w systemie Rzymskim. Leonardo z Pizy podróżował przez wiele lat po ówczesnym świecie śródziemnomorskim ucząc się różnych zagadnień od arabskich matematyków. Jednak historia zera znacznie wyprzedziła okres przypadający na życie Fibonacciego i sięga głęboko dalej niż jego podróże, dlatego musimy cofnąć się w czasie trochę wcześniej.
 
Leonardo Pisano (Fibonacci)

Początki zera

 
Już prawdopodobnie 4000 lat temu cywilizacja sumeryjska wykorzystywała puste przestrzenie w formie naszej dzisiejszej „spacji”, żeby odnotować brak. Jednak pierwszy odnotowany przypadek użycia „zero” przypada na III wiek przed naszą erą i dotyczy starożytnego Babilonu(2). W systemie babilońskim zero odpowiadało dwóm małym trójkącikom i służyło mniej więcej do odróżnienia liczb dziesiętnych w taki sam sposób jak zero jest wykorzystywane w dniu dzisiejszym przy odróżnianiu dziesięć, sto, tysiąc (10, 100, 1000) itd.(3). Co ciekawe bardzo podobny symbol zaczął być wykorzystywany przez cywilizację Majów na kontynencie amerykańskim, około 350 roku naszej ery. Majowie w przeciwieństwie do Babilończyków wykorzystywali swoje „zero” w kalendarzu(4). Te trzy przykłady to wczesne przypadki użycia znaku odnotowującego „brak”. Jednak nie są uznawane za dokładne odzwierciedlenie zera. Puste miejsce jest prawdopodobnie pewną formą interpunkcji, umożliwiającą właściwy odczyt pozostałych liczb(5). Użytkowanie „zera” jednak nie było całkowicie ograniczone i wyizolowane wyłącznie do tych cywilizacji ze względu na przenikanie się kultur i wiedzy. W 130 r. naszej ery Ptolemeusz wykorzystuje babiloński sześć dziesiątkowy system liczbowy w swoim „Mathematike Syntaxis” (Almagest)(6) i używa znacznika „braku” w formie „O”. Świadczy to, że dzięki bliskości cywilizacji babilońskiej znano pojęcie „braku” również w Europie.
 
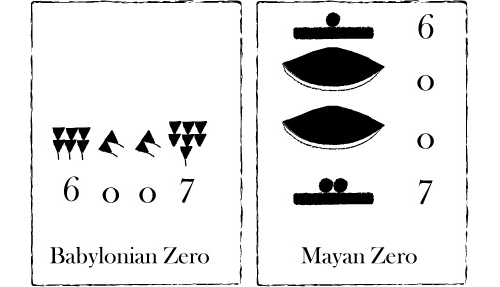Babilońskie „zero” i „zero” Majów

Równoległe badania nad zerem

 
Wczesne systemy numeryczne znały „zero” jako część systemu w którym zapisywano liczby, natomiast nie jako liczbę z osobnymi właściwościami, które reprezentowały by wartość. Jednak był pewien kraj, bardziej położony na wschód niż ziemie Perskie. Były to Indie, gdzie narodził się system liczbowy, który wyewoluował do postaci wyrafinowanego systemu, z którego korzystamy dziś. Co ciekawe mitologia indyjska wzmiankuje użycie zera w formie jaką znamy dziś już 17000 lat przed naszą erą(7). Około 500 roku naszej ery Aryabhata wynalazł system liczbowy, który nie posiadał zera i był systemem pozycyjnym. Jednak co jest znaczące dla tej inwencji to, to, że używał słowa „ka” aby nazwać pozycję liczby w tabeli. Dokładnie tym samym słowem określono potem zero. Co ciekawe Hindusi również stosowali wcześniejszą wersję „zero” w celu oznaczenia pustego miejsca, czyli „braku” liczby. Tak samo robiły to cywilizacje mezopotamskie. Najwcześniejszy określony zapis zero w indyjskiej matematyce, który odpowiada dzisiejszej definicji tej liczby, a co do którego wszyscy badacze są bezsprzecznie zgodni, przypada na rok 876 naszej ery(8). Jednak zero zaczęto stosować wcześniej. Zaraz po tym jak się pojawiło stało się przedmiotem dyskusji i logicznych przemyśleń. Trzej astronomowie i matematycy indyjscy, którzy starali się znaleźć odpowiedzi na pytania związane z właściwością zera jako liczby, mieli na imię Brahmagupta, Mahavira i Bhaskara.
 
Matematycy indyjscy wykorzystywali małe kropeczki pod numerami, żeby zaznaczyć „brak”. Brahmagupta starał się ustalić zasady arytmetyczne dla działań zawierających zero i w końcu doszedł do wniosku, że mając daną liczbę, jeżeli odejmiemy ją od siebie to wtedy otrzymamy zero. Opisywał to w następujący sposób:
 

Suma liczby ujemnej i zero jest ujemna. Suma liczby dodatniej i zero jest dodatnia. Suma zero i zero wynosi zero.

 
Następnie przechodził do odejmowania.
 

Liczba ujemna odjęta od zero jest dodatnia, dodatnia liczba odjęta od zero jest ujemna, zero odjęte od liczby ujemnej jest ujemne, zero odjęte od liczby dodatniej jest dodatnie, zero odjęte od zera to zero.

 
W 830 roku, czyli około 200 lat po Brahmagupcie, Mahavira napisał swoje dzieło pod tytułem „Ganita Sara
Samgraha”, w którym idzie o krok dalej i rozwija przemyślenia Brahamgupty.
 

Liczba pomnożona przez zero wynosi zero. Liczba pozostaje bez zmian, kiedy zero zostaje od niej odjęte.

Brahmagupta

Zero rusza w świat

 
Zanim w Indiach dalej kontynuowano rozwijanie idei zera, koncepcja ta przeniósła się dalej na wschód w kierunku Chin oraz na zachód w kierunku państw islamskich. W krajach arabskich koncepcją zera zainteresował się matematyk Mohammed ibn-Musa al-Khowarizmi i to właśnie on był pierwszym, który usystematyzował hinduską arytmetykę. W swoich pracach pokazał jaką funkcję może pełnić zero w równaniach algebraicznych. Dzięki al-Khowarizmi, zero od IX wieku naszej ery zaczęto stosować na dobre, w arabskim systemie numerycznym. A jako jego reprezentację przyjęto formę owalną, którą używamy po dziś dzień (9).
 
W ten oto sposób historia zatacza koło i wraca do Leonardo z Pizy, sławnego Fibonacciego, który około 1200 roku po porwocie ze wcześniej wspomnianych podróży napisał dzieło pt. „Liber Abaci”, w którym opisał dziewięć hinduskich symboli matematycznych, oraz zero. Co ciekawe Fibonacci nie traktuje zero na równi z resztą symboli (1,2,3,4,5,6,7,8,9) jako, że dziewięć symboli nazywa liczbami, natomiast zero, określa po prostu zerem. Dalsza historia tej liczby w Europie wyraża się tym, że koncepcja „zera” jeszcze przez długi czas po Fibonaccim, nie była w powszechnym zastosowaniu.
 
Gerolamo Cardano, w późniejszym okresie rozwiązywał skomplikowane równania, w dalszym ciągu bez użycia zera(10). Zero do powszechnego użytku weszło dopiero w okresie Baroku i zadomowiło się do dziś.
 

Przypisy

8) http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Zero.html
9) http://www-history.mcs.st-andrews.ac.uk/Biographies/
Al-Khwarizmi.html
10) http://google.books